[기계학습 심화] Linear Classification review

Linear Classification

살짝 복습으로
우리는 예측값을 구하기 위해 함수를 찾으려는 것이고,
Linear에서는 W, b를 찾는 것이 목적이다.

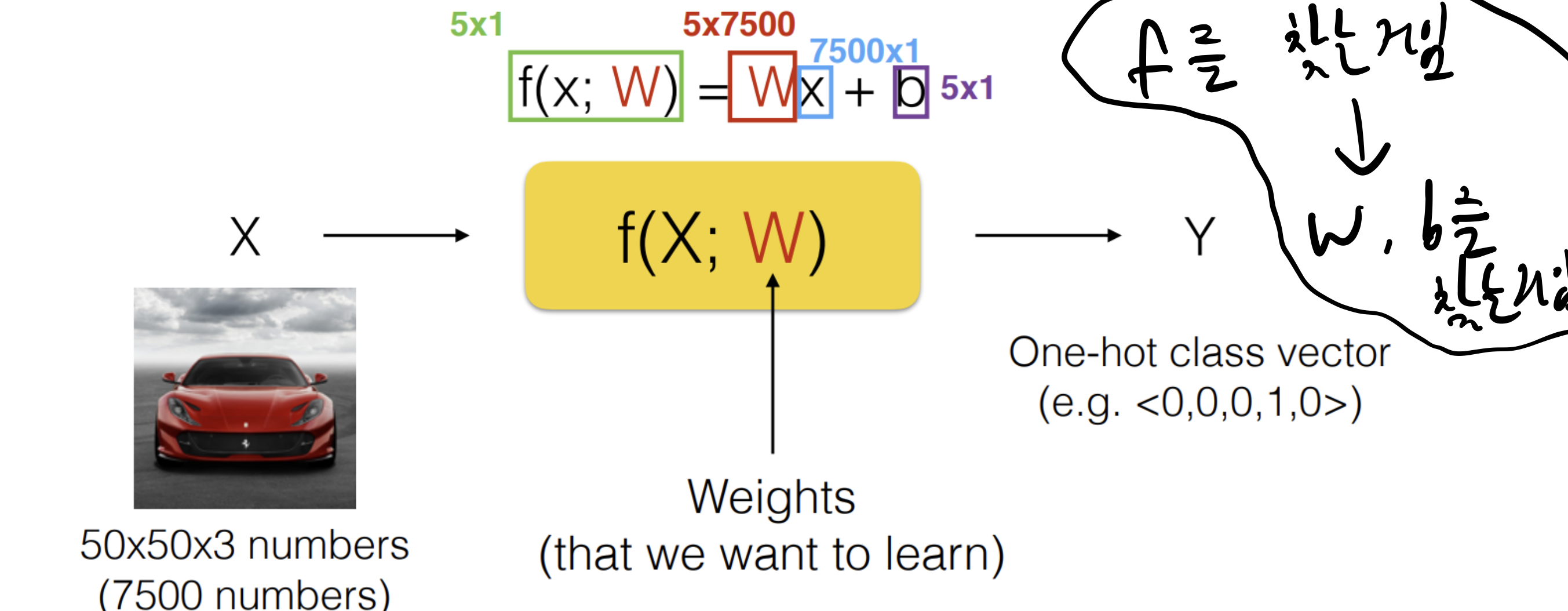
최적의 W, b를 찾기 위해 Loss 개념을 사용해
train data에서 가장 실제값을 잘 표현하는 W, b를 찾는 것이다.

부가적으로 직접 설정해야 하는 hyper parameter 값을 잘 설정하기 위해서는 validation data를 사용

Loss Function

Loss Function - L1 Loss

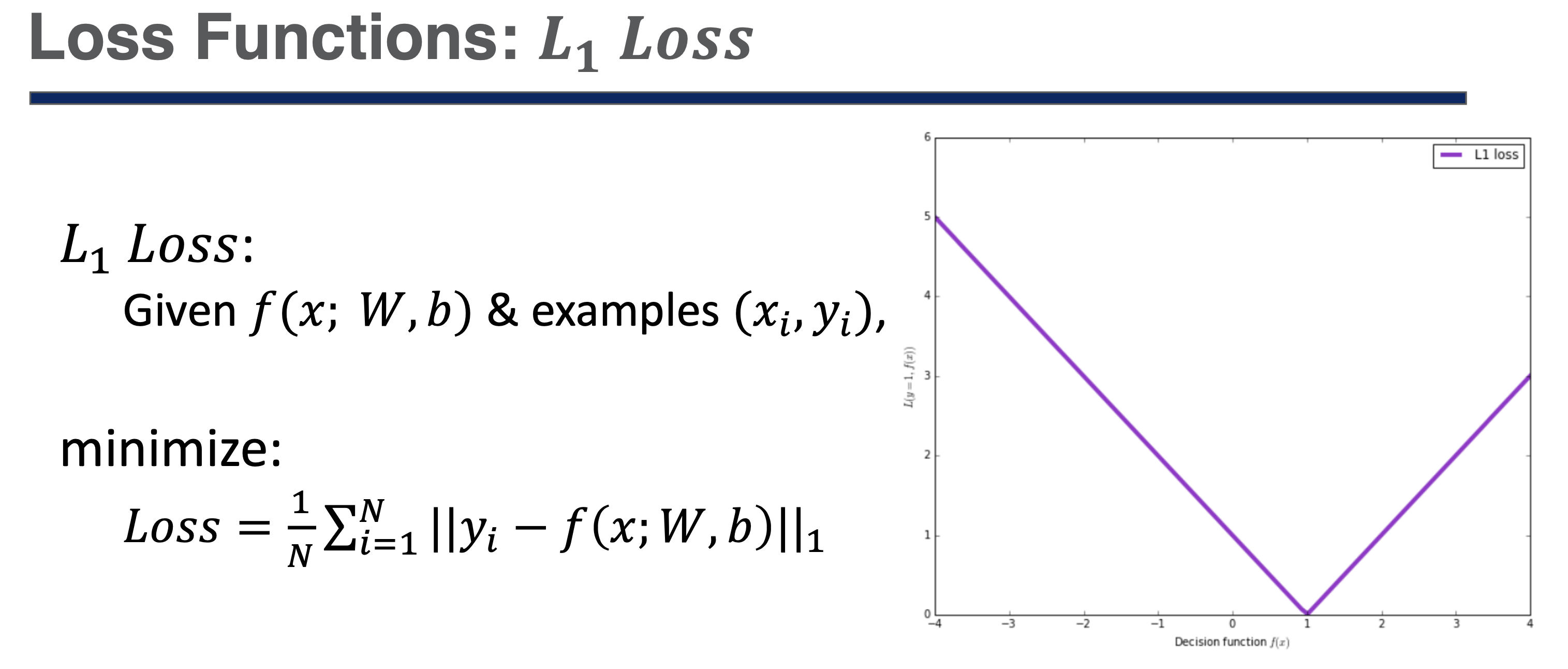
정답이 1일때 예측값이 1이면 에러가 0
간단하다.

Loss Function - L2 Loss

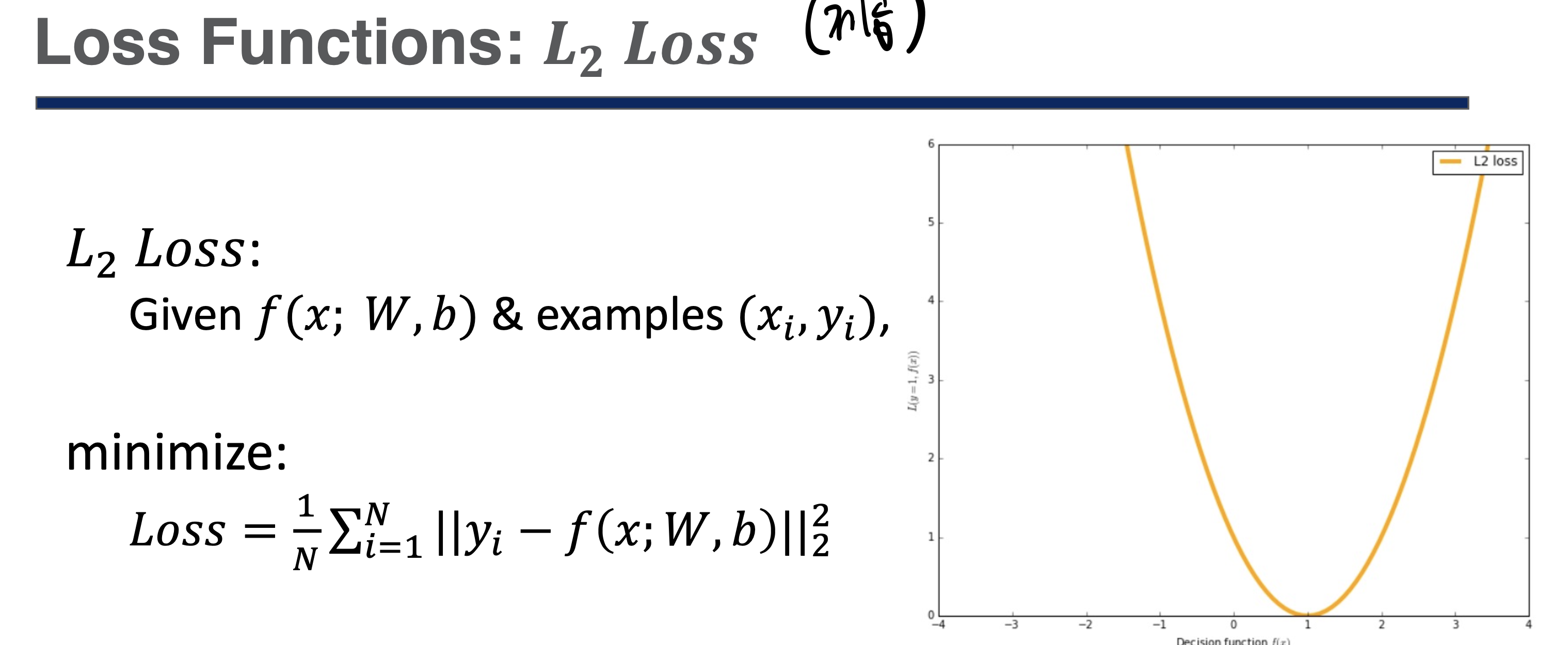
이것도 간단하다 L1에서 제곱

Loss Function - Cross Entropy Loss

비교

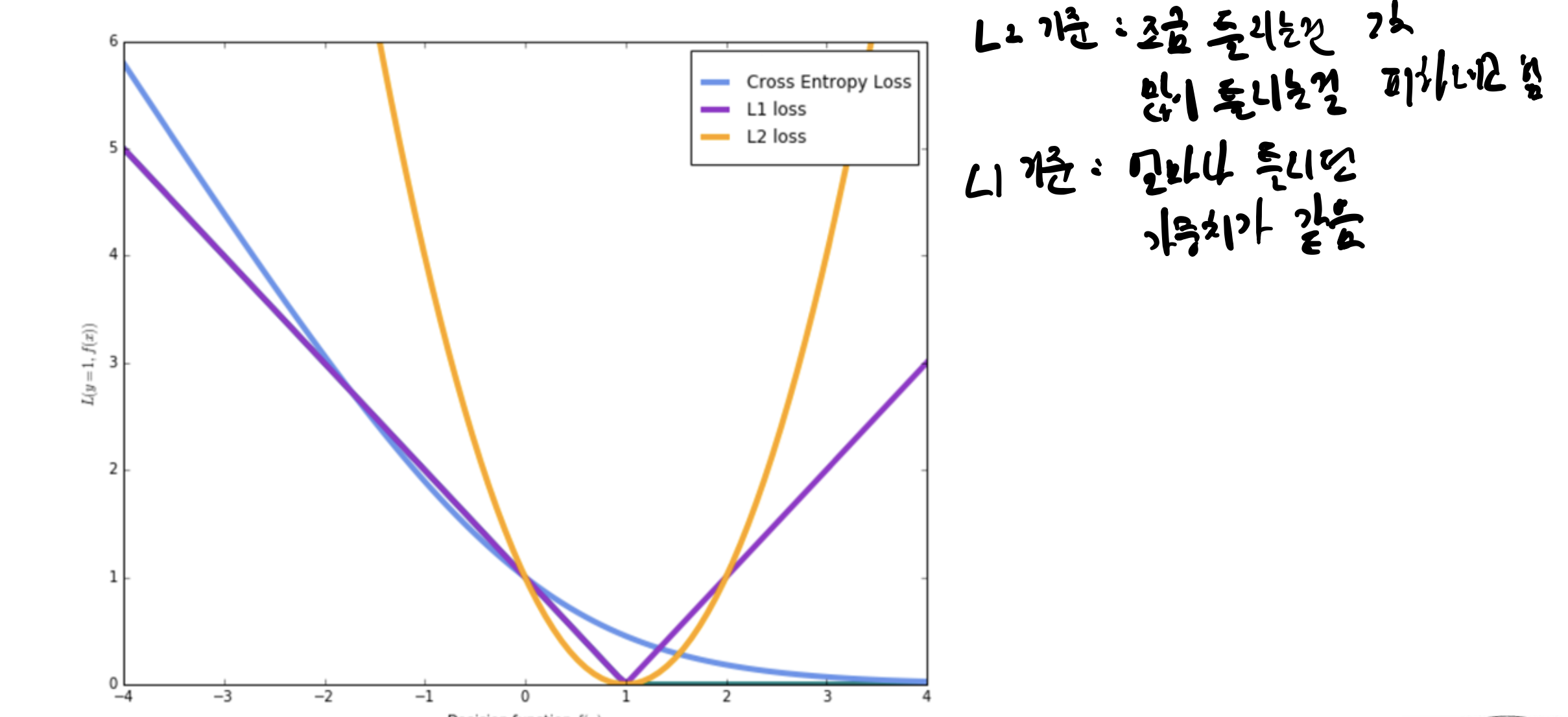
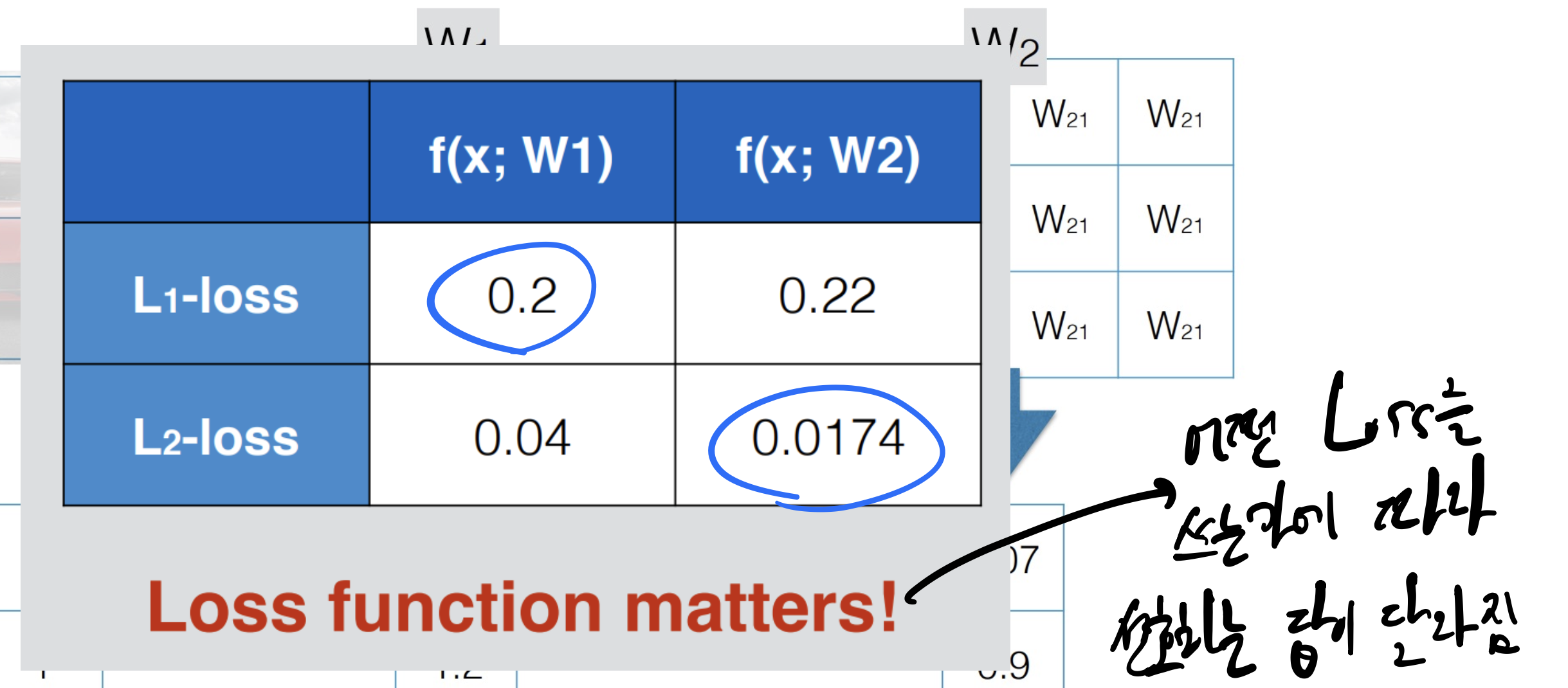
어떤 Loss Function을 사용하는가에 따라
예측값이 달라지는 모습

Overfitting, Underfitting

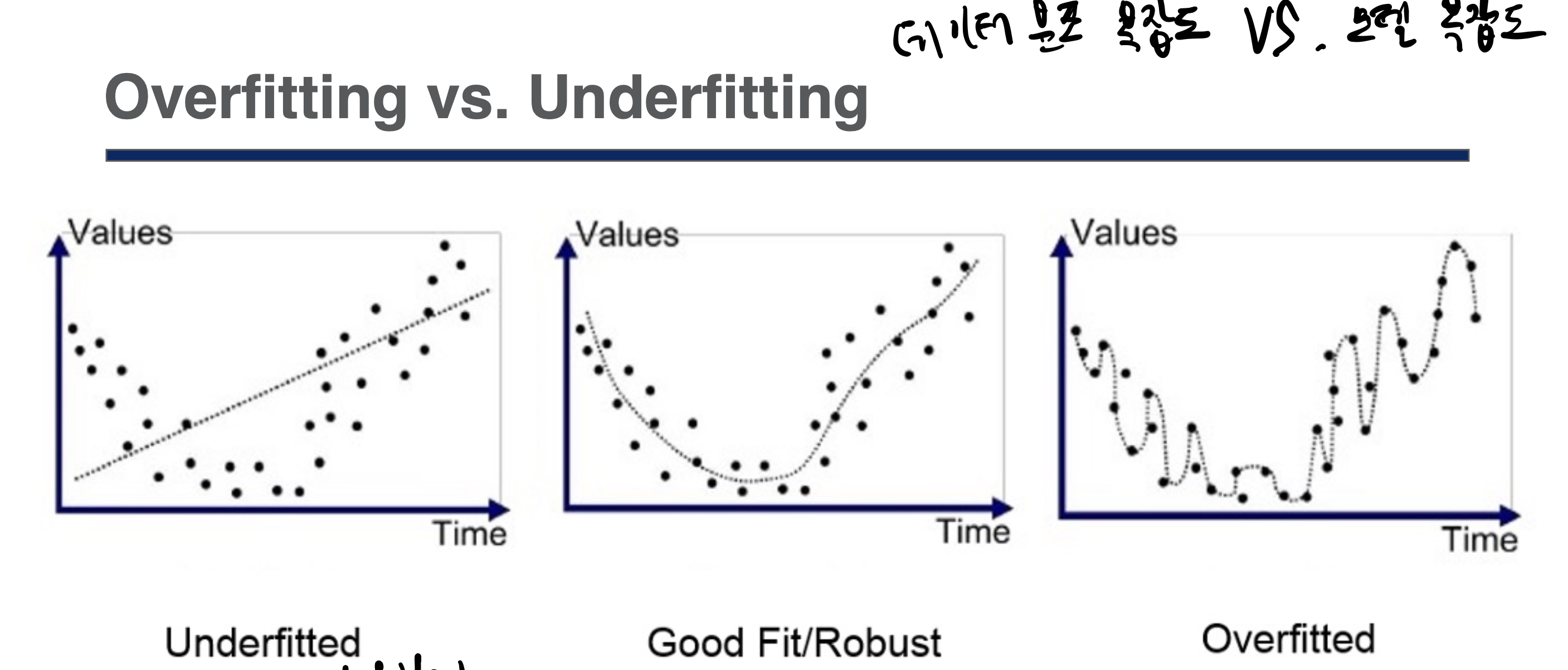
쉽게 Underfitting은 모델 복잡도가 부족한 경우
데이터 복잡도에 비해

Overfitting은 모델 복잡도가 과한 경우
(파라미터 개수가 너무 많다)
데이터 복잡도에 비해

overfitting 경우에는 training data에 너무 딱맞아서
예측능력이 없다라고 할 수 있다.
(global 트렌드를 따라가지 못한다)

Regularization - Overfitting 방지

한국어로 정규화!

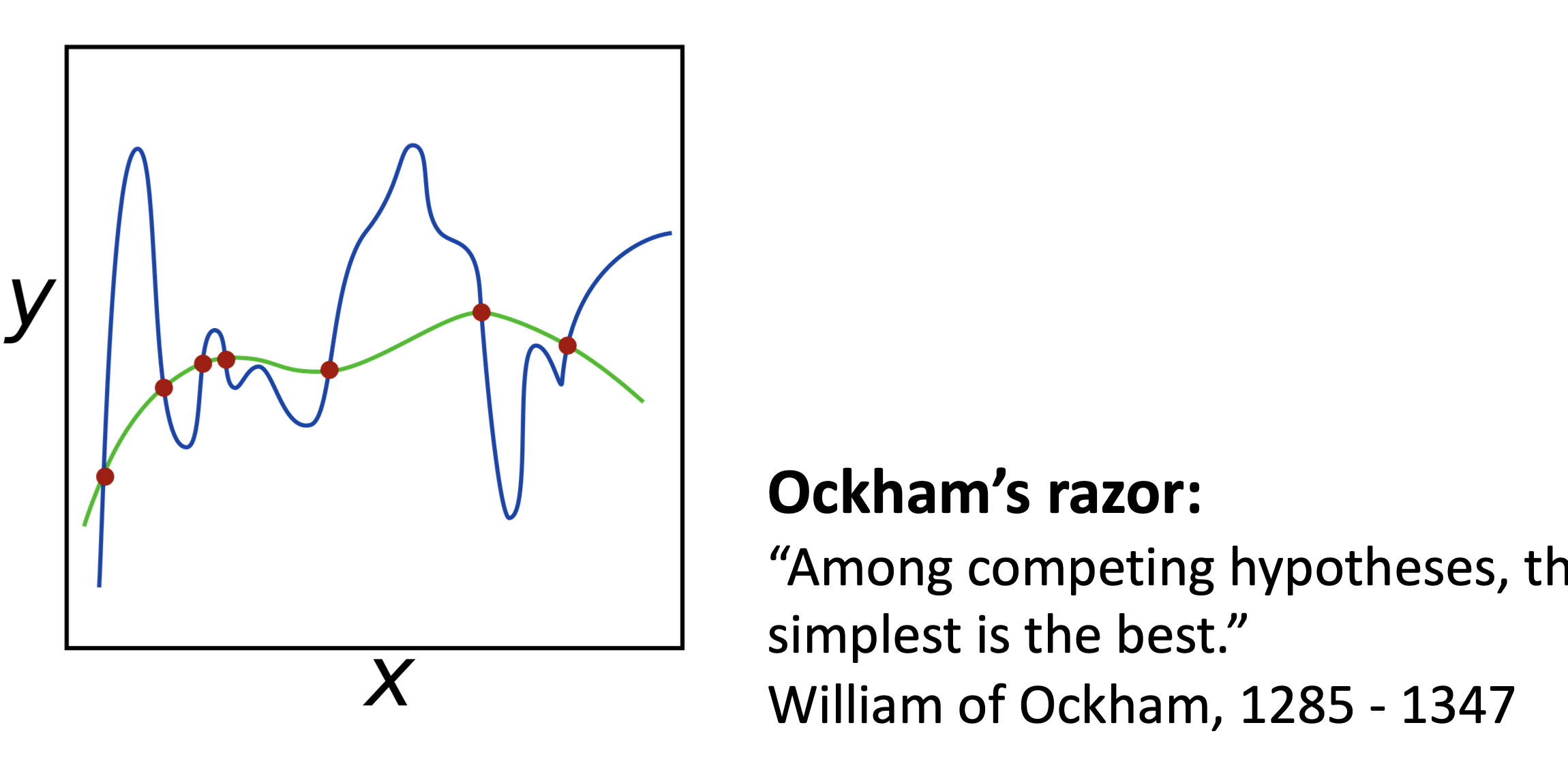
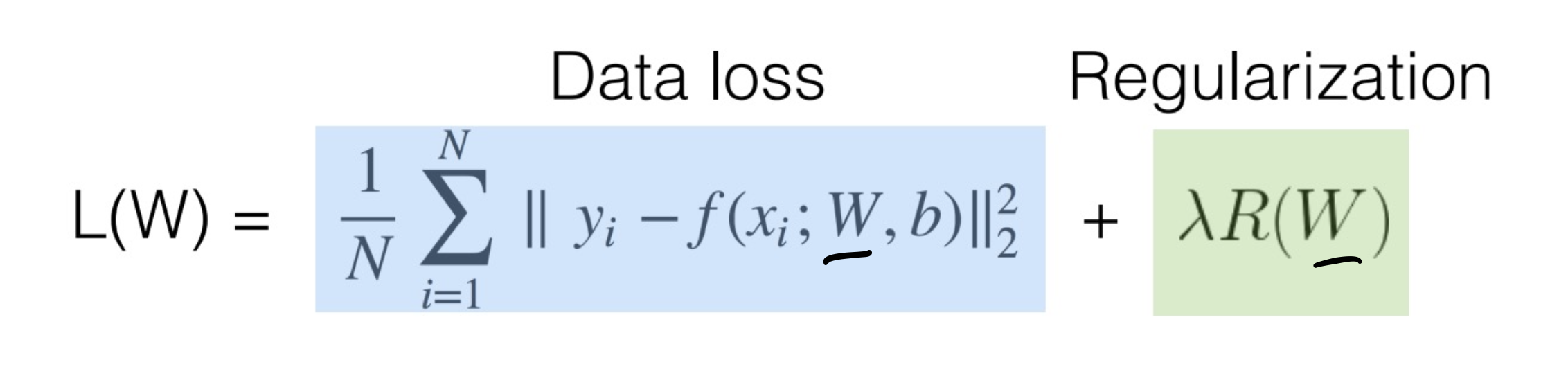
방법론적으로
loss를 최소화 하려고 하지만, 그걸 좀 방해하는 계수를 추가하는 것이다.

Optimization

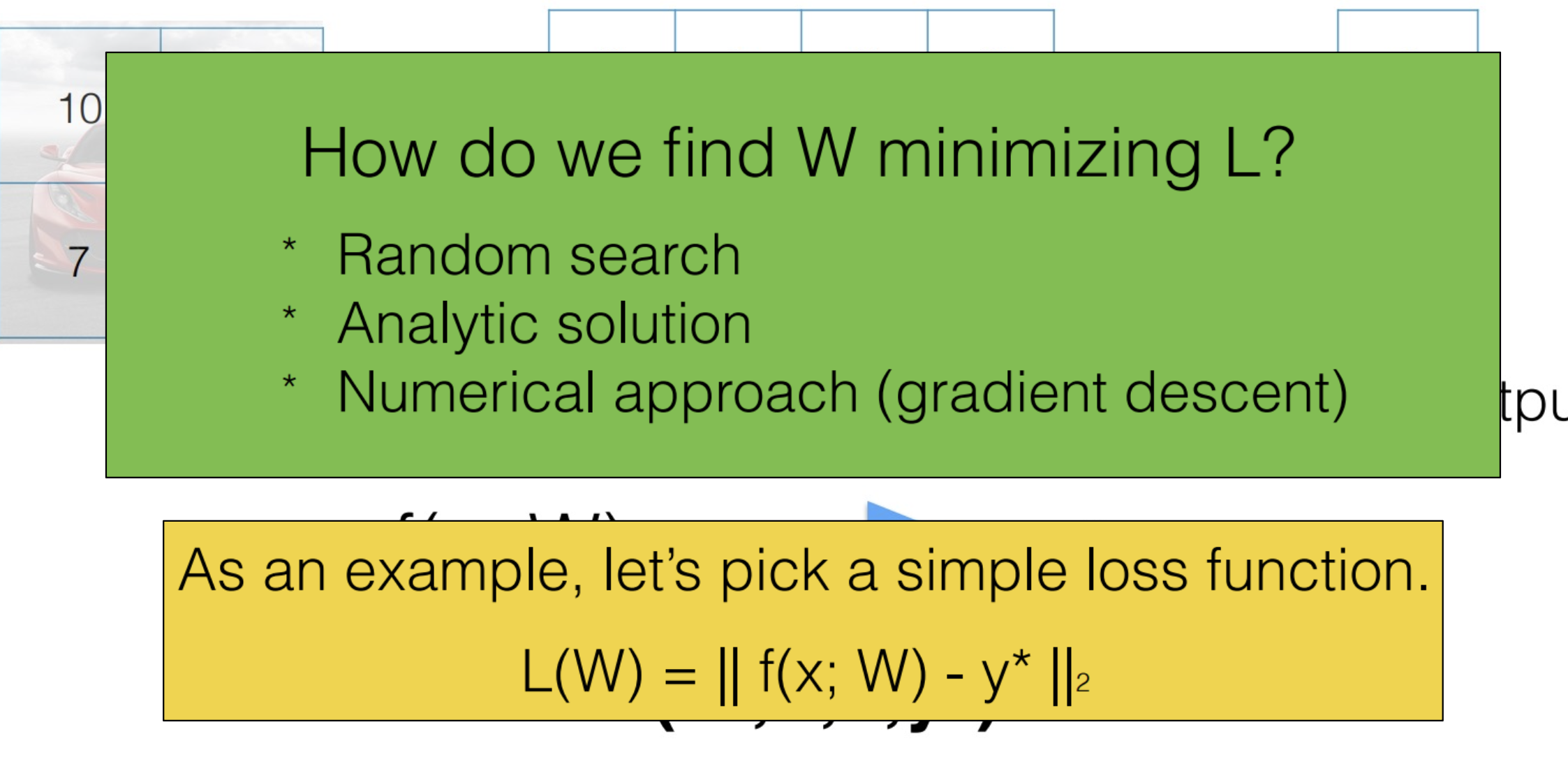
1. Random Search 말그대로 랜덤하게 파라미터를 만들어서 가장 잘 맞는 파라미터를 찾는 것
   느리다는 단점이 있다.
   

2. Analytic Solution Loss값을 최소화 시키는 W, b를 구하는 것
   Loss(W, b) 미분값 = 0인 값을 찾는 방법을 사용했었다
   Linear Regression에서는 괜찮은데
   복잡하면 사용하지 못한다

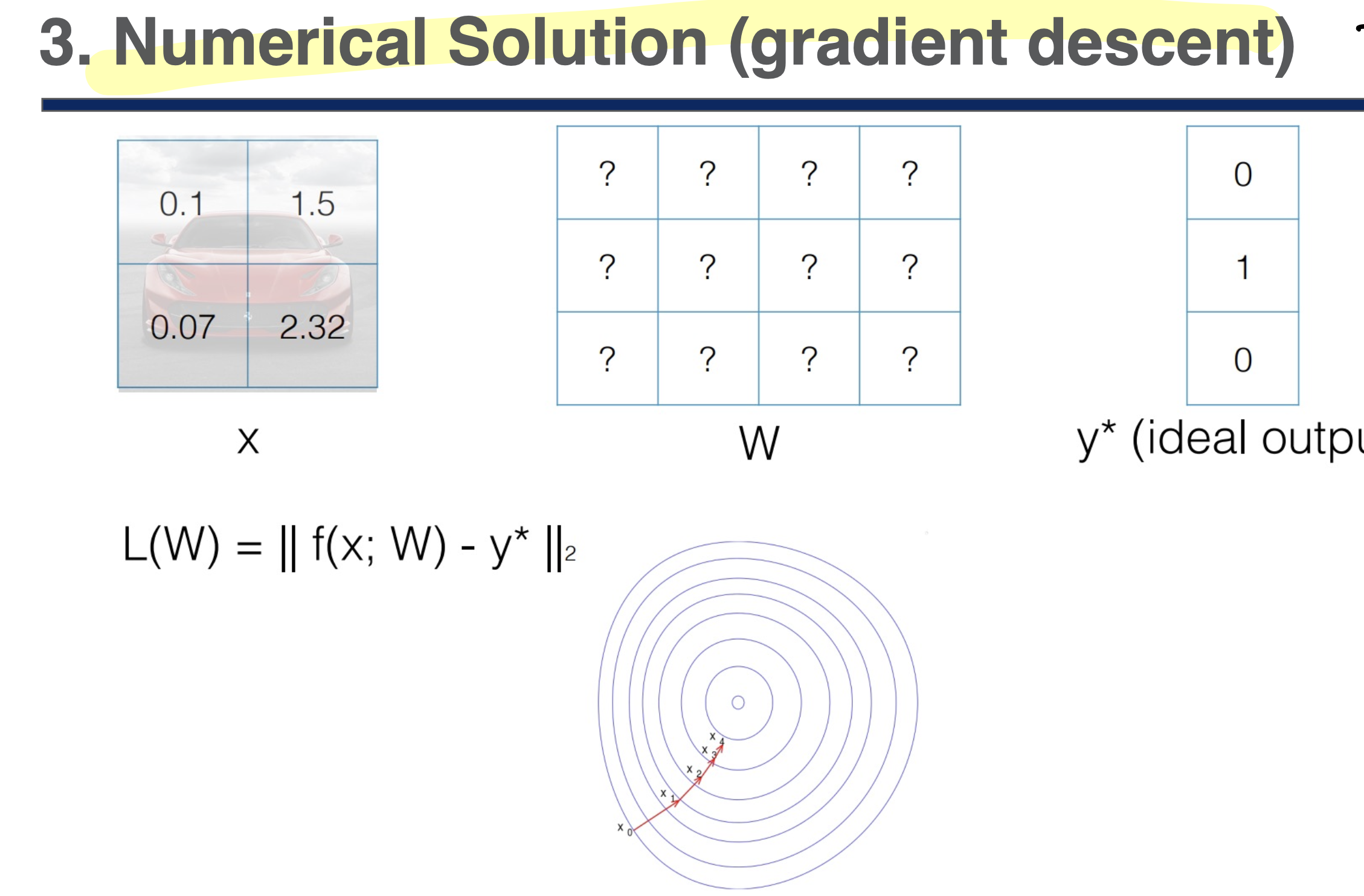
3. Numerical Solution 미분값을 근사적으로 구하는 방법
   Gradient Descent 방법을 사용한다
   (기울기의 반대 방향으로 계속 움직여서 최적 값을 찾는 방법)
   Local mnimum에 빠질 수 있다